\[\require{physics} \renewcommand{\vec}[1]{\underline{#1}} \renewcommand{\exp}{\text{e}} \DeclareMathOperator*{\argmin}{argmin}\]

Homework 1

Topic

Homework regarding the first week. The goal is to work with basic numerical approximation of PDE’s’ and functions.

Bram Lagerweij
18 Feb 2021

1 Method of Lines

Consider the one-dimensional advection diffusion equation:

\[{u}_{t} + c{u}_{x} - \mu{u}_{xx} = 0 \qquad \forall \, x \in \Omega = [0, 1] \quad \& \quad t>0\]

where \(\mu>0\) is the diffusion coefficient and \(c\) the wave speed. Consider periodic boundary conditions and the following initial condition:

\[u(x,0) = \sin(2\pi x)\]

What do we expect the exact solution to do? Due to the advective part, the initial condition travels at constant speed to the right. At the same time, due to the diffusive term, the initial condition is dissipated at a rate that depends on \(\mu\).

Consider the following discretization. Use second-order central finite differences to approximate \(u_x\) and \(u_{xx}\). Use forward and backward Euler to obtain full discretization (write down the schemes). Consider a fixed mesh with of \(\Delta x\).

1.1 Advective Diffusive PDE

Consider a final time of \(t=1\), \(c=1\) and \(\mu=0.01\). For each full discretization proceed as follows:

1. Experiment using the following time step sizes: \(\Delta t = 10^{−4},\, 10^{−3}\) and \(10^{−2}\).

2. How do the explicit and implicit methods behave for these time steps?

There is a so called Courant-Friedrichs-Lewy condition that formulates a condition of stability on the model:

\[C = \frac{c\Delta t}{\Delta x} \leq C_{\max}\]

Where \(C_{\max}\) is a constant, which for explicit schemes, such as forward Euler, is around 1. If the condition is violated the method becomes unstable, that does not mean that the results are unstable from the first iteration.

Fig. 1 : The forward difference scheme is unstable for \(dt=10^{-2}\), the backward scheme behaves as expected. Click here for an animated version.

Fig. 2 : With a timestep of \(dt=10^{-3}\) both the forward and backward Euler scheme are stable. Click here for an animated version.

Fig. 3 : As expected with a timestep of \(dt=10^{-4}\) both time integrations behave stable. Click here for an animated version.

r"""
Solving an Advective and Diffusive PDE with finite differences.

The PDE described by

.. math::
    u_{t} + u_{x} = \mu u_{xx}  \quad \forall x \in\Omega = [0, 1]  \;\; \& \;\;  t > 0

With a periodic boundary condition. It will show a combination of diffusive
and advective behaviour. The approximation used is a second order finite
difference scheme in space with both a forward and backward Euler method of
lines implementation to handle the time direction.

The goal is to implement the code in python and not rely on existing solvers.

Bram Lagerweij
COHMAS Mechanical Engineering KAUST
2021
"""

# Importing External modules
import sys
import matplotlib.pyplot as plt
import numpy as np

# Importing my own scripts
sys.path.insert(1, '../src')
from finitedifference import advectivediffusive
from solvers import forwardEuler, backwardEuler


if __name__ == '__main__':
    # Define properties.
    dx = 1e-2
    dt = 1e-4
    t_end = 1
    mu = 0.01  # Diffusive term
    c = 1  # Advective term

    # Define discrete ranges.
    dof = int(1 / dx) + 1
    x, dx = np.linspace(0, 1, dof, retstep=True)
    t = np.arange(0, t_end + dt, step=dt)

    # Prepare solver.
    u0 = np.sin(2 * np.pi * x)  # Initial condition

    # Solve the problem using method of lines.
    u_forw = forwardEuler(advectivediffusive, u0, dt, t_end, args=(dof, dx, mu, c))
    u_back = backwardEuler(advectivediffusive, u0, dt, t_end, args=(dof, dx, mu, c))

    # Plotting the results.
    plt.xlim(0, 1)
    plt.xlim(0, 1)
    plt.ylim(-1, 1)
    plt.xlabel('$x$ location')
    plt.ylabel('$u(x)$')
    plt.annotate('time t={}'.format(t[-1]), xy=(0.5, 0.9), ha='center')
    plt.tight_layout()

    plt.plot(x, u_forw, label='forward')
    plt.plot(x, u_back, label='backward')

    plt.legend()
    plt.show()

1.2 Advective PDE

Consider \(\mu=0\) and \(c=2\) and solve the PDE using the explicit and the implicit methods. Use \(\Delta t = 10^{−4}\) and solve the problem for the following final times \(t=1,\, 5,\, 10,\, 15\) and \(20\). Comment on the behaviour of each full discretization as the final time increases.

Fig. 4 : Even with small time steps this type of hyperbolic like equation can become unstable when using a forward Euler method. Click here for an animated version.

Due to the region of convergence of the forward Euler method such a hyperbolic PDE with no dissipation will always be unstable. In the animation the instabilities become only clear after 14 seconds. Nevertheless, even at \(t=1\) the method should be considered unstable. Similarly the backward Euler is inaccurate as well, it is too dissipative, after 20 seconds around 20% of our, wave magnitude has disappeared.

r"""
Solving an Advective PDE with finite differences.

The PDE described by

.. math::
    u_{t} + u_{x} = 0  \quad \forall x \in\Omega = [0, 1]  \;\; \& \;\;  t > 0

With a periodic boundary condition. The approximation used is a second order
finite difference scheme in space with both a forward and backward Euler method
of lines implementation to handle the time direction.

The goal is to implement the code in python and not rely on existing solvers.

Bram Lagerweij
COHMAS Mechanical Engineering KAUST
2021
"""

# Importing External modules
import sys
import matplotlib.pyplot as plt
import numpy as np

# Importing my own scripts
sys.path.insert(1, '../src')
from finitedifference import advective
from solvers import forwardEuler, backwardEuler


if __name__ == '__main__':
    # Define properties.
    dx = 1e-2
    dt = 1e-4
    t_end = 20
    c = 2  # Advective term

    # Define discrete ranges.
    dof = int(1 / dx) + 1
    x, dx = np.linspace(0, 1, dof, retstep=True)
    t = np.arange(0, t_end + dt, step=dt)

    # Prepare solver.
    u0 = np.sin(2 * np.pi * x)  # Initial condition

    # Solve the problem using method of lines.
    u_forw = forwardEuler(advective, u0, dt, t_end, args=(dof, dx, c))
    # u_back = backwardEuler(advective, u0, dt, t_end, args=(dof, dx, c))

    # Plotting the results.
    plt.xlim(0, 1)
    plt.ylim(-1, 1)
    plt.annotate('time t={}'.format(t[-1]), xy=(0.5, 0.9), ha='center')
    plt.tight_layout()

    plt.plot(x, u_forw, label='forward')
    # plt.plot(x, u_back, label='backward')

    plt.legend()
    plt.show()

2 Approximation of functions

Consider the function:

\[f(x) = \sin^4(2\pi x) \qquad \forall \, x \in \Omega = [0, 1]\]

for which we have to find multiple global and local approximations. Let \(f_h (x)\) be such an approximation for a given grid. We consider the following errors:

\[E_1 := \int_\Omega | f(x) - f_h(x) | dx \quad \text{and} \quad E_2 := \int_\Omega \big(f(x) - f_h(x)\big)^2 dx\]

2.1 Global Approximations

Consider the following approximations all with \(N\) terms:

1. the Taylor series around \(x=0.5\),

2. the Fourier series,

3. a global polynomial interpolation on the closed interval given by:

\[f_h(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_{N-1} x^{N-1}\]

Consider different levels of refinement, \(N=4,\, 5,\, 6,\,\dots,\,10\) and for each approximation report both \(E_1\) and \(E_2\).

2.1.1 Taylor series

The Taylor series till the order \(N\) is defined through:

\[f_h(x) = \sum_{n=0}^N \frac{f^{(n)}(x_0)}{n!} (x - x_0)^n\]

Which immediately got me into problems, analyzing the \(n\)-th derivative of a function is a numerically a pain. Quickly the round off errors become significant, and from the 5th derivative onward the basic scipy Taylor series function became useless. As a result I decided to hardcode the weighting constants in our expansion, these are obtained from manual derivatives.

Fig. 5 : Approximating \(f(x)\) with a Taylor series centered around \(x_0=0.5\) till order 10.

From Fig. 5 it can be observed that the Taylor series is not a very efficient approximation. At the boundary of our domain the error is very high.

2.1.2 Fourier series

The Fourier series, which we assume to be real, approximates the equation with:

\[f_h(x) = \sum_{n=0}^N c_n\exp^{\frac{2\pi n x}{P}i} + \bar{c}_n\exp^{-\frac{2\pi n x}{P}i}\]

where \(P\) is the period of the function \(f(x)\) and \(c_n\) are complex valued coefficients that can be found through a Fourier Transform. In our case I used a FFT algorithm to find these coefficients from our discrete dataset, essentially the real-FFH tries to solve:

\[c_n = \sum_{n=0}^{K} x_k \exp^{\frac{2\pi k n}{K-1}} \qquad n = 0, \dots, N\]

in a highly efficient manner. Notice that for each unknown \(c_n\) consists of a real and imaginary part. This does mean that this approximation for any given \(N\) is more complex. The resulting approximation is shown in Fig. 6. Which show that this series is highly efficient in the approximation of our function. This is not to surprising, after all we are approximation a trigonometric functions with a series of trigonometric functions it is likely that we find the exact function somewhere in our series.

Fig. 6 : Approximating \(f(x)\) with a Fourier series seems to be exact from the fourth order.

2.1.3 Polynomial series

The polynomial series

\[f_h(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_{N-1} x^{N-1}\]

was to be found with a fitting through \(N\) evenly spaced points \(x_i\) throughout this interval. It should be noted that this type of fitting can be rewritten as an minimization:

\[\argmin_{a_0, \dots, a_{N-1}} \sum_{i=0}^N \big( f(x_i) - f_h(x_i) \big)^2\]

\[\qq{that means: find} a_0, \dots a_{N-1} \qq{such that} f(x_i) - f_h(x_i) = 0 \quad \forall x_i\]

This minimization can efficiently be casted to a system of equations and subsequently be solved. This system of equations has \(N\) unknowns and \(N\) functions, and because each of these functions is linearly independent a solution exists. Simply said we construct a polynomial that goes exactly through these \(N\) points.

Fig. 7 : Approximating \(f(x)\) with a polynomials of order \(N-1\) using \(N\) sample points.

One can also choose to use more sample points to evaluate the minimization problem, lets consider that we use \(M\) sample points. It is not generally possible to find a \(N-1\) order polynomial to fit exactly through more then \(N\) points. But we can find the best polynomial, to be specific one that minimizes:

\[\argmin_{a_0, \dots, a_{N-1}} \sum_{i=0}^M \big( f(x_i) - f_h(x_i) \big)^2\]

Which is as if we are minimizing our error \(E_2\) at only discrete points, instead of solving the integral itself. Anyway, Fig. 8 shows this fit would look like. The results seems closer, because we’re not just minimizing the error at \(N\) points but at \(5N\) points.

Fig. 8 : Approximating \(f(x)\) with a polynomials of order \(N-1\) using \(M=5N\) sample points.

2.1.4 Comparison

For the comparison of these different approximations I’ve plotted the errors on a log scale. Please do note that the Fourier series has 2 times as many unknowns for the \(N\) compared to the other methods.

Fig. 9 : The error \(E_1\) for our different approximations where the approximation order ranges from 1 to 20.

Fig. 10 : The error \(E_2\) for our different approximations where the approximation order ranges from 1 to 20.

I assume that the error of the Taylor series is increasing because the higher order terms will cause higher errors at the boundaries of our domain. But all in all it is my opinion that the Taylor series is a bad approximation for this purpose, it is difficult to calculate due to the derivatives and the result is inaccurate. This is not so surprising however, Taylor series are meant to approximate the behaviour of a function around a given point \(x_0\) to characterize the local behaviour. We are here using it on a relatively large domain.

The script used for these computations can be found at 3 GlobalApproximation.py.

2.2 Local Approximations

Split the domain \(\Omega\) into \(N\) cells. For each cell \(K\), compute linear and quadratic approximations \(f_K(x)\) where \(f_K(x_i)=f(x_i)\) where \(x_i\) are evenly spaced gridpoints, including the boundaries of the cell. Compute and report both \(E_1\) and \(E_2\) for a different numbers of cells \(N=4,\, 5,\, 6,\,\dots,\,10\).

The approximation by linear elements is created by scaling hat (shape) functions appropriately. These functions are chosen in such a way that:

1. The sum of all the shape functions together equals one, \(\sum_{n=1}^{N} \varphi_i(x) = 1\) This is called the Partition of Unity Method.

2. There where a single function reaches its maximum all the other functions equal zero.

Then our approximation is defined by:

\[f_h(x) = \sum_{n=1}^N w_n \varphi_n(x)\]

where the weights \(w_n\) are unknown. But because the shape function where chosen smartly these weights are independent. After all at the point where a single shape function reaches its maximum (1) the other functions are zero. As a result the weight of this shape function equals the value of the function we are trying to approximate at the center point of the shape:

\[w_n = f(X_n)\]

where \(X_n\) denotes the point where shape function \(\varphi_n(x)\) reaches its maximum.

2.2.1 Linear Elements

In the case of linear elements these shape functions are defined as:

\[\begin{split}\varphi_n(x) = \begin{cases} 0 \quad &\forall \quad 0 &\leq x \leq &X_{n-1} \\ \frac{x - X_{n-1}}{X_{n} - X_{n-1}} \quad &\forall\quad X_{n-1} &\leq x \leq &X_{n}\\ 1 - \frac{x - X_{n}}{X_{n+1} - X_{n}} \quad &\forall \quad X_{n} &\leq x \leq &X_{n+1}\\ 0 \quad & \forall \quad X_{n+1} &\leq x \leq &L \end{cases}\end{split}\]

where \(X_n\) is the node of this shape function, \(X_{n-1}\) and \(X_{n+1}\) the nodes surrounding ours.

A more efficient formulation includes the creation of a unit function that is rescaled depending on the locations of the nodes. But I haven’t yet implemented such an function yet.

Fig. 11 : The function \(4\sin(\pi x) + 1\) approximated with four elements. The first element contain the orange and half of the green shape function.

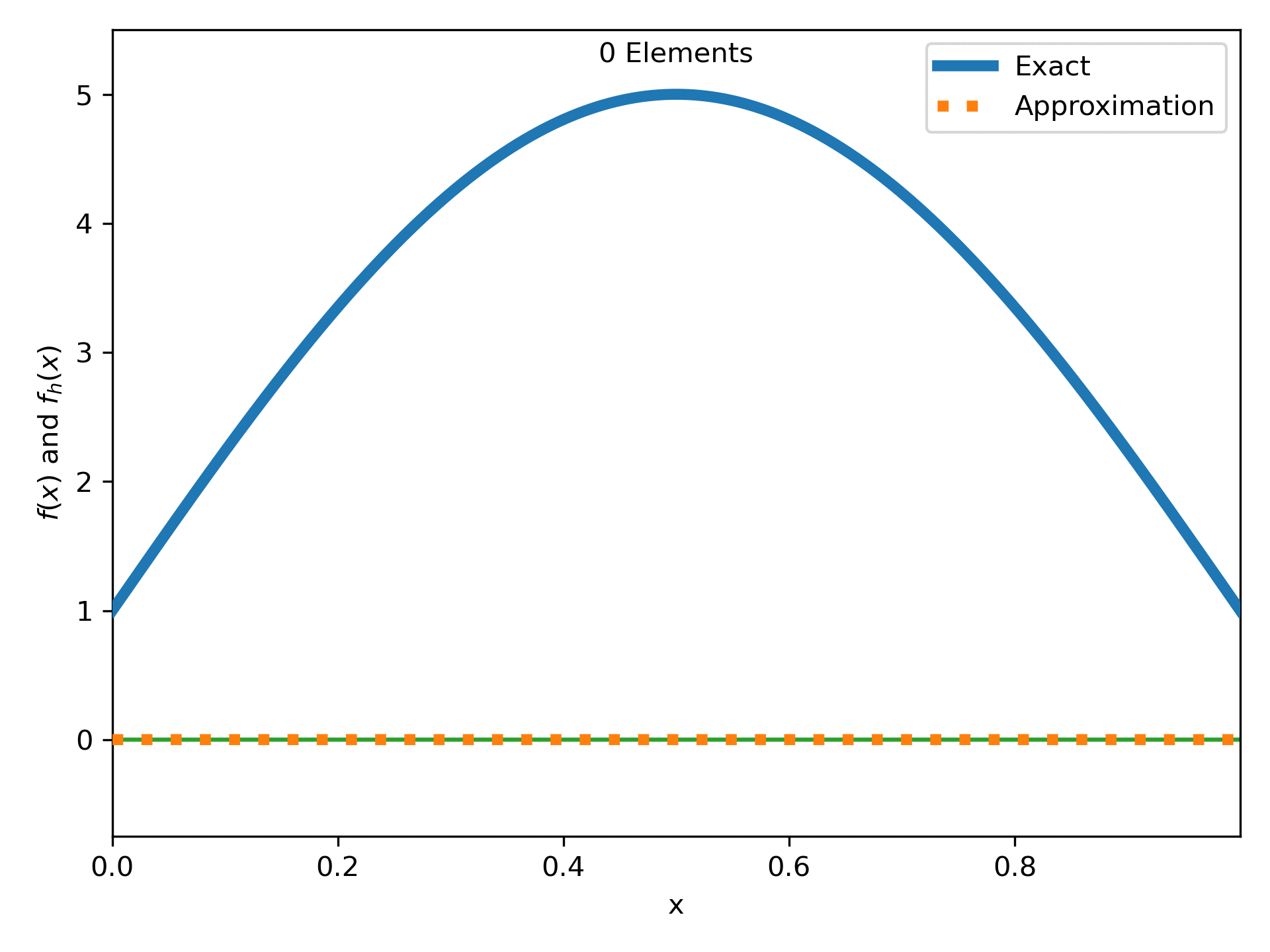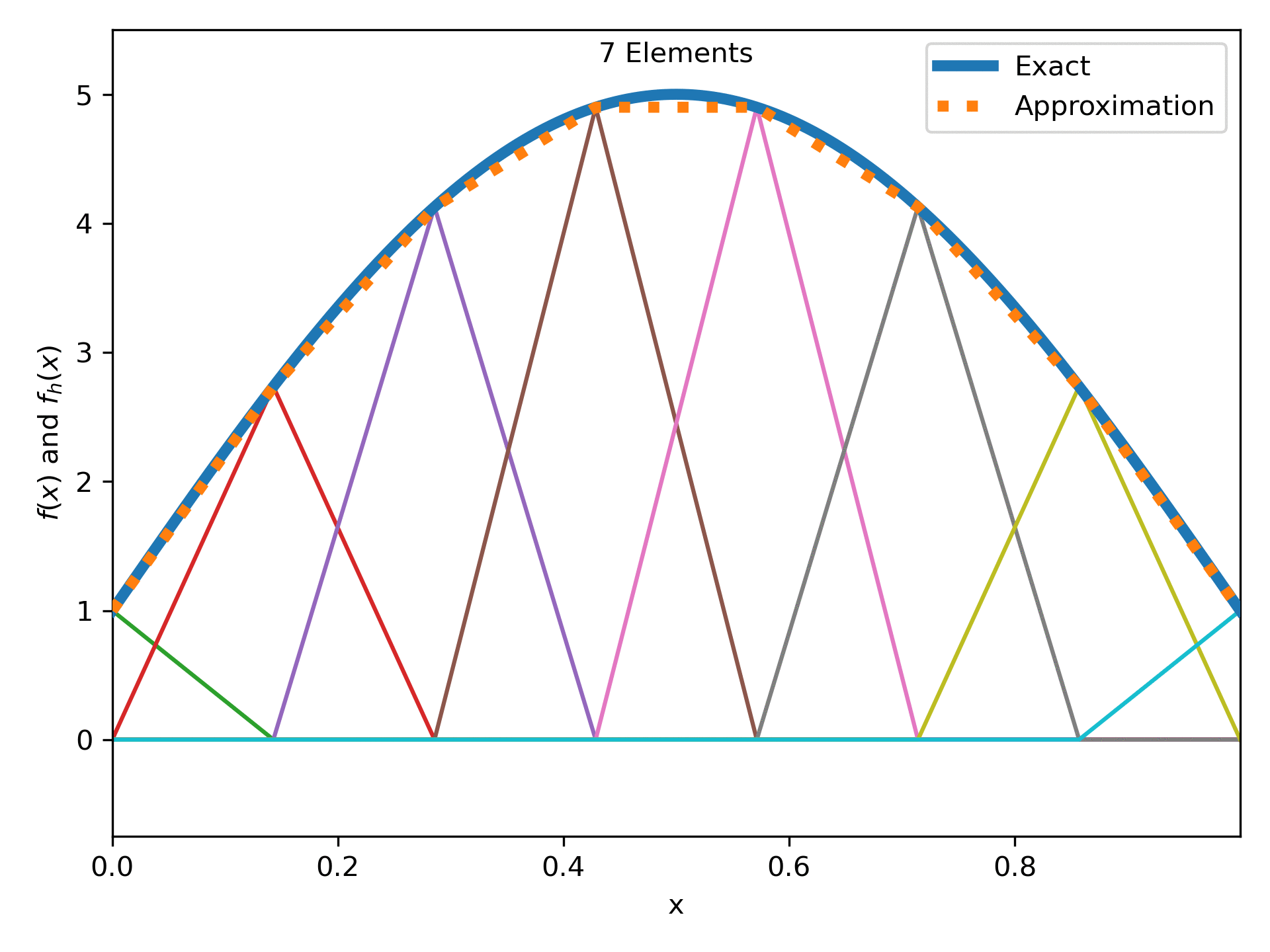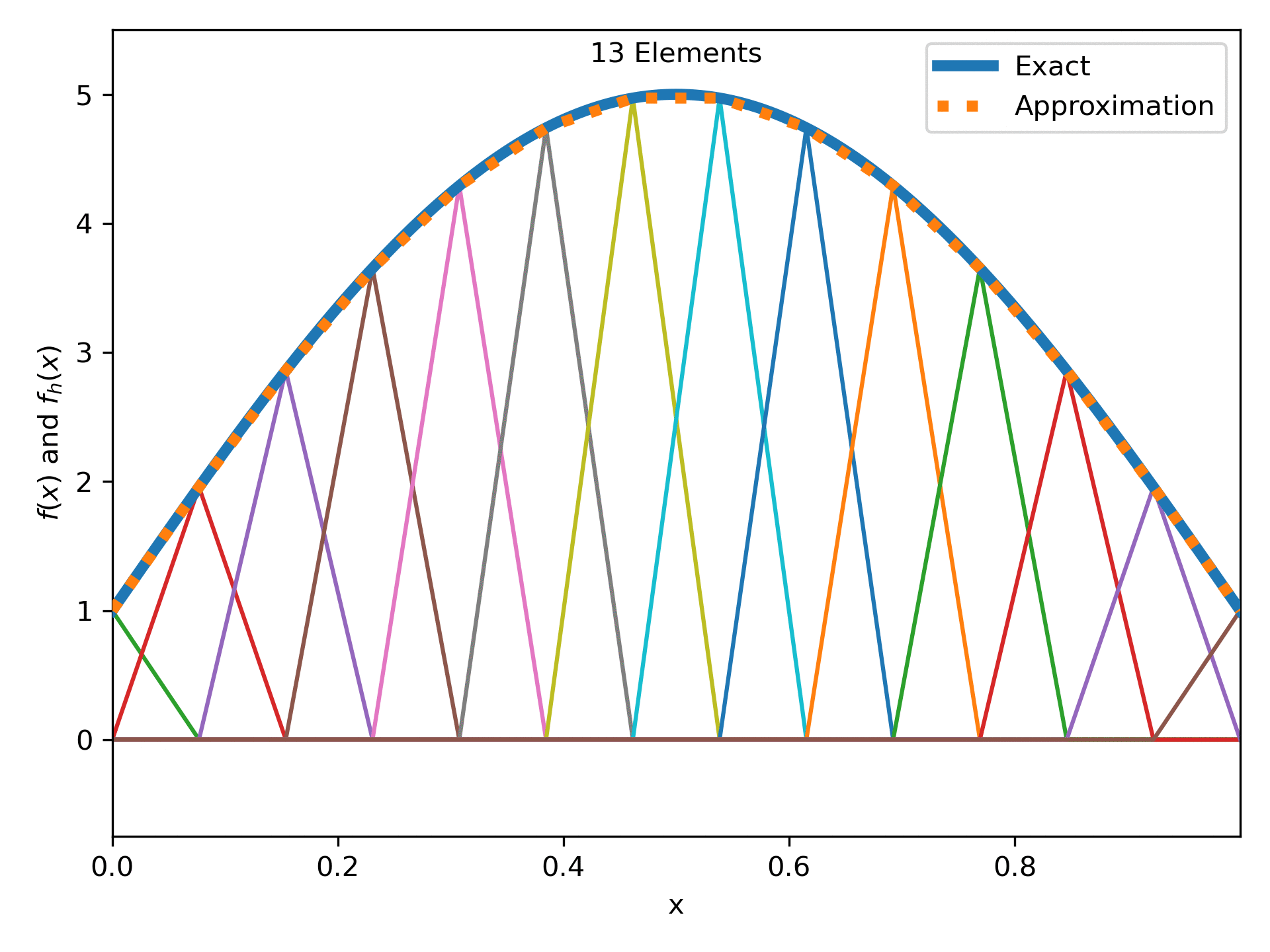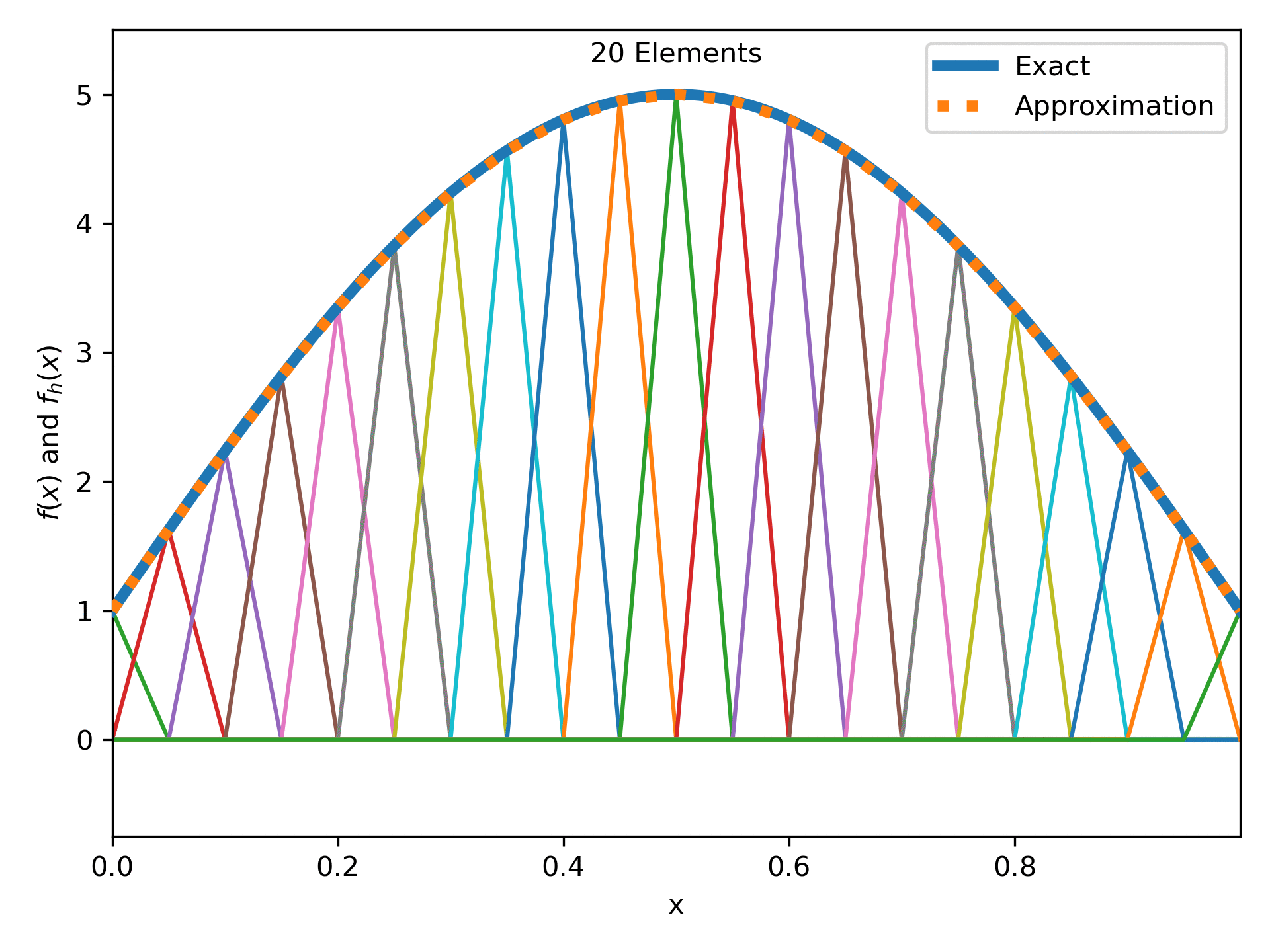
Fig. 12 : The function \(4\sin(\pi x) + 1\) approximated more and more linear elements.

Fig. 13 : The approximation of \(f(x)\) with linear elements.

2.2.2 Quadratic Elements

In the case of quadratic elements there are two different types of shape function. One of these function extents into two elements, similar to what the linear element does. The second shape function is only inside a single element, and on an interior node. This node is placed exactly in the middle between the start and end of the element. I’ll give these nodes the subscripts \(n-\frac{1}{2}\) and \(n+\frac{1}{2}\). Now the shape functions are defined by:

\[\begin{split}\varphi_n(x) &= \begin{cases} 0 \quad &\forall \quad 0 &\leq x \leq &X_{n-1} \\ \frac{2}{(X_n - X_{n-1})^2} (x - X_{n-1})(x - X_{n-\frac{1}{2}}) \quad &\forall\quad X_{n-1} &\leq x \leq &X_{n}\\ \frac{2}{(X_{n+1} - X_{n})^2}(x - X_{n+1})(x - X_{n+\frac{1}{2}}) \quad &\forall \quad X_{n} &\leq x \leq &X_{n+1}\\ 0 \quad & \forall \quad X_{n+1} &\leq x \leq &L \end{cases}\\ \varphi_{n-\frac{1}{2}} (x) &= \begin{cases} 0 \quad &\forall \quad 0 &\leq x \leq &X_{n-1} \\ -\frac{4}{(X_n - X_{n-1})^2} (x - X_{n-1})(x - X_{n}) \,\, \quad &\forall\quad X_{n-1} &\leq x \leq &X_{n}\\ 0 \quad & \forall \quad X_{n+1} &\leq x \leq &L \end{cases}\end{split}\]

Again a more efficient formulation includes the creation of a unit function that is rescaled depending on the locations of the nodes. But I haven’t yet implemented such an function yet.

Fig. 14 : The function \(4\sin(\pi x) + 1\) approximated with four elements. The first element contain the orange and half of the green shape function.

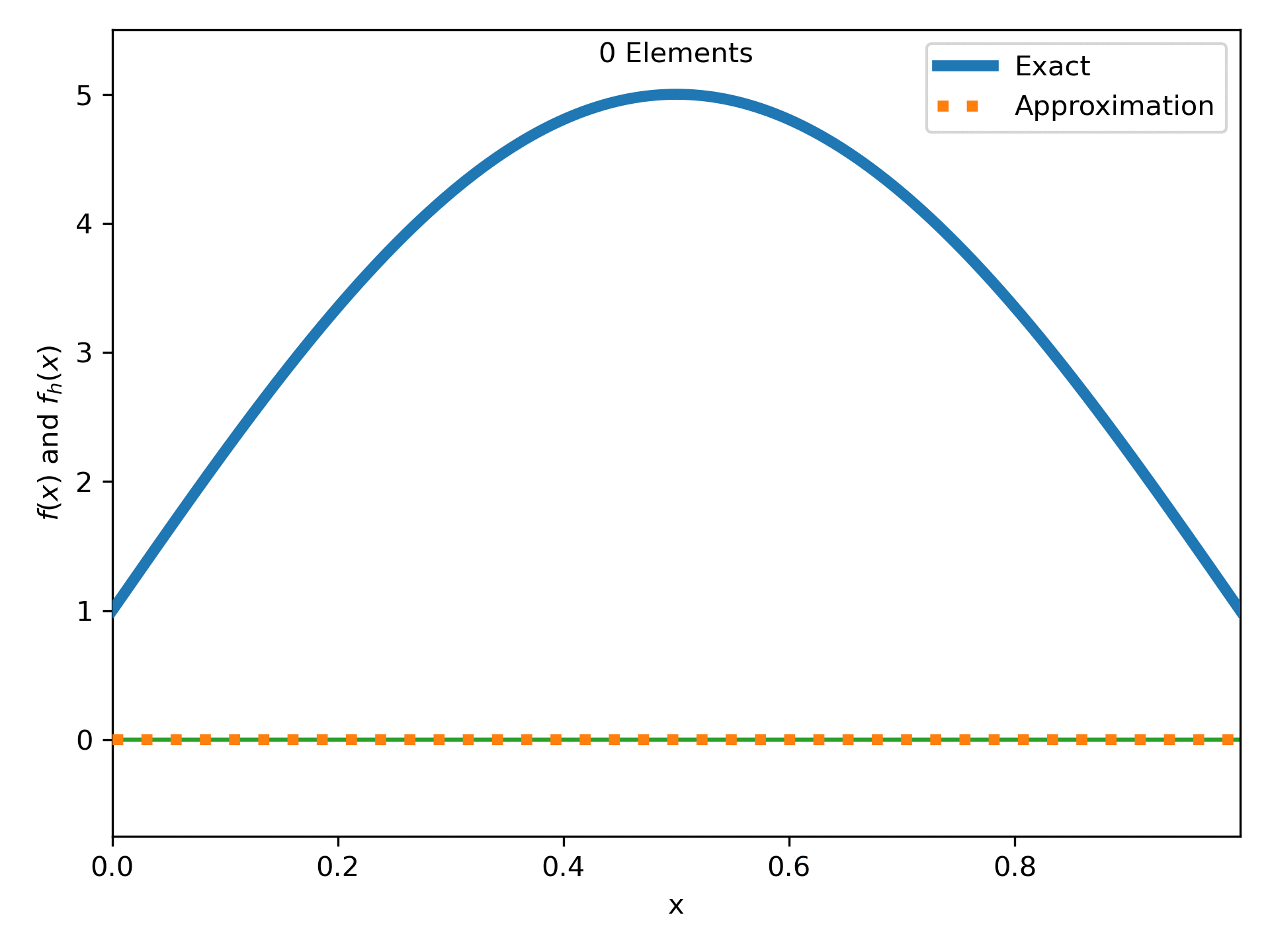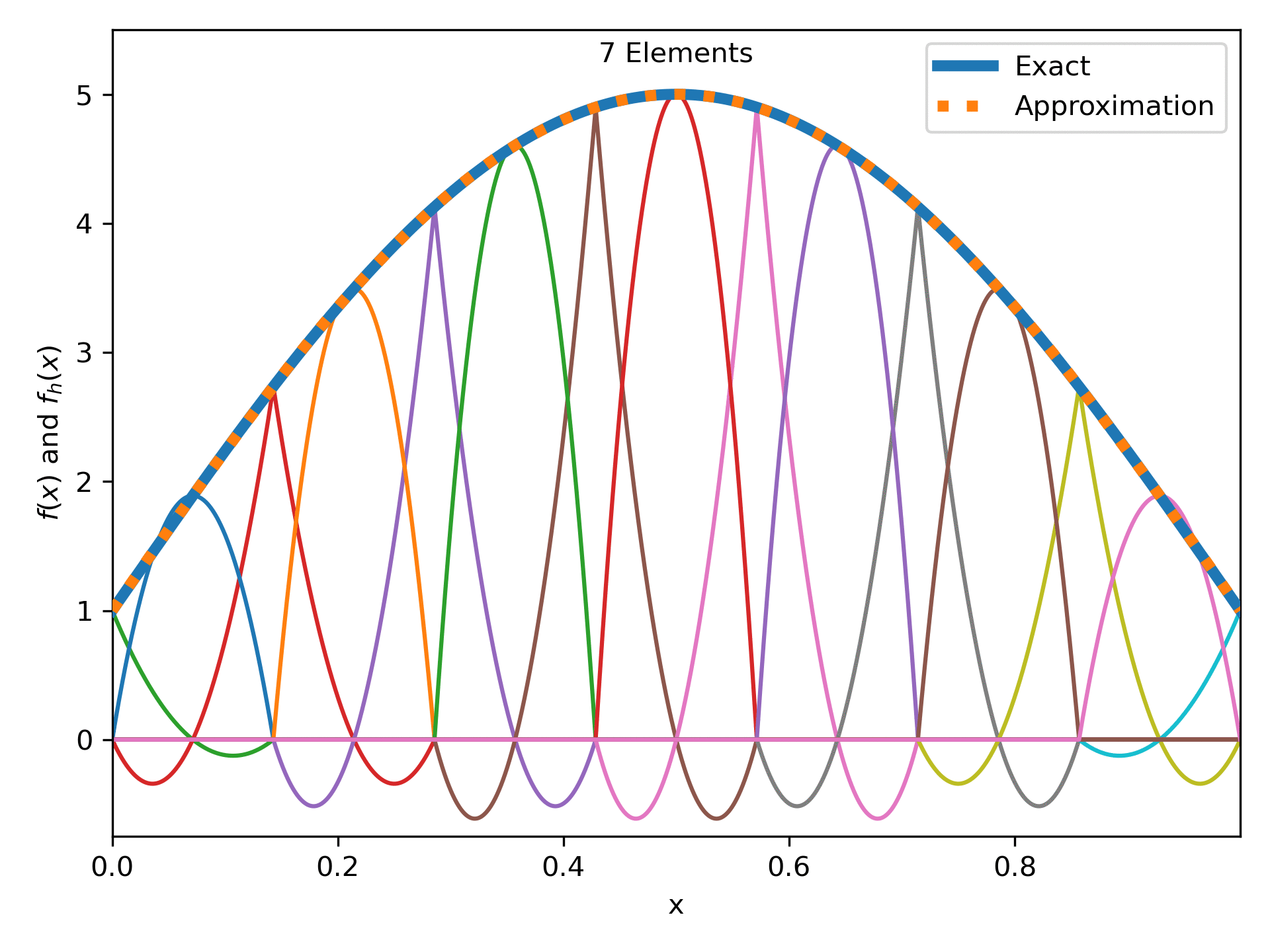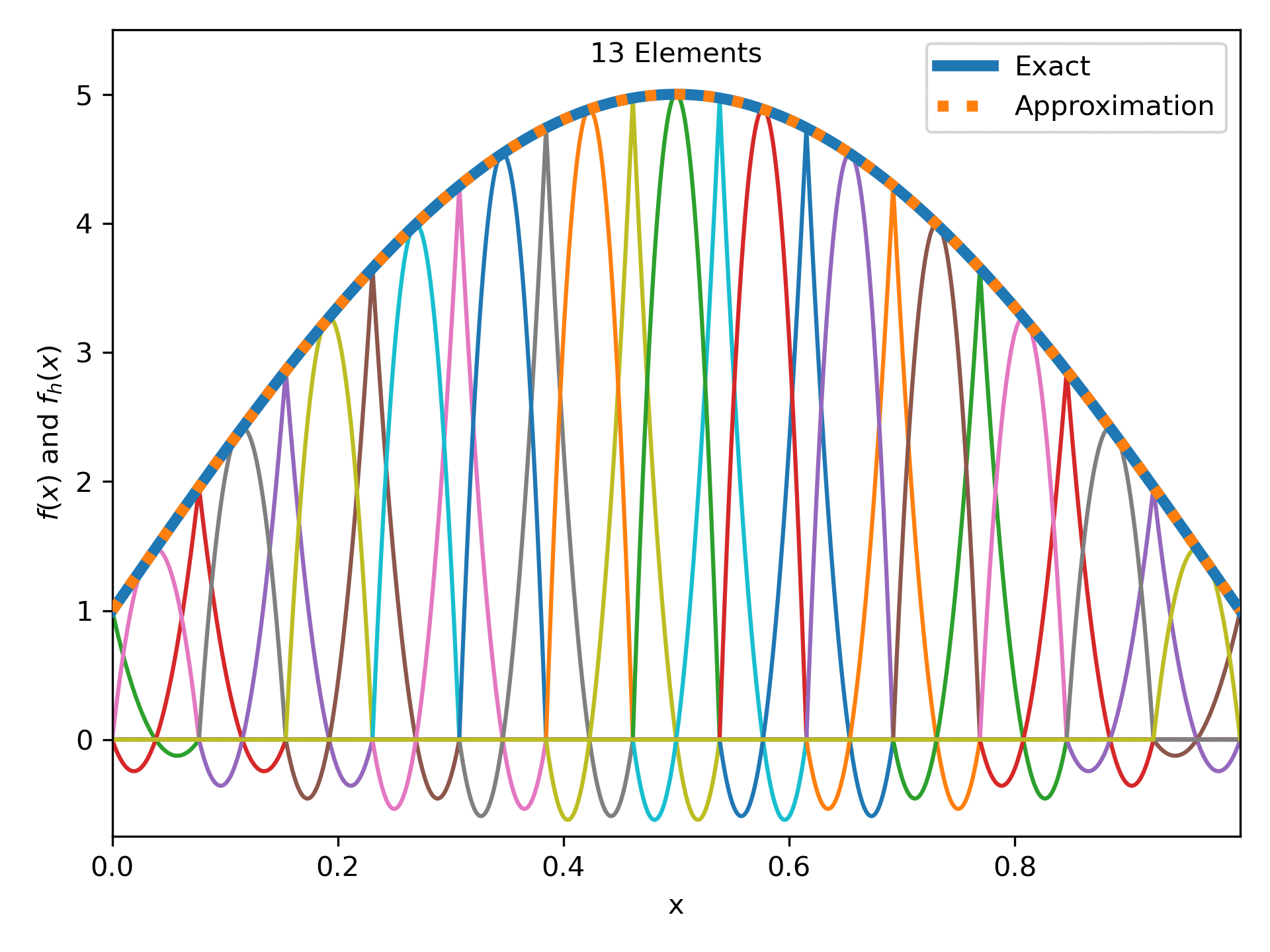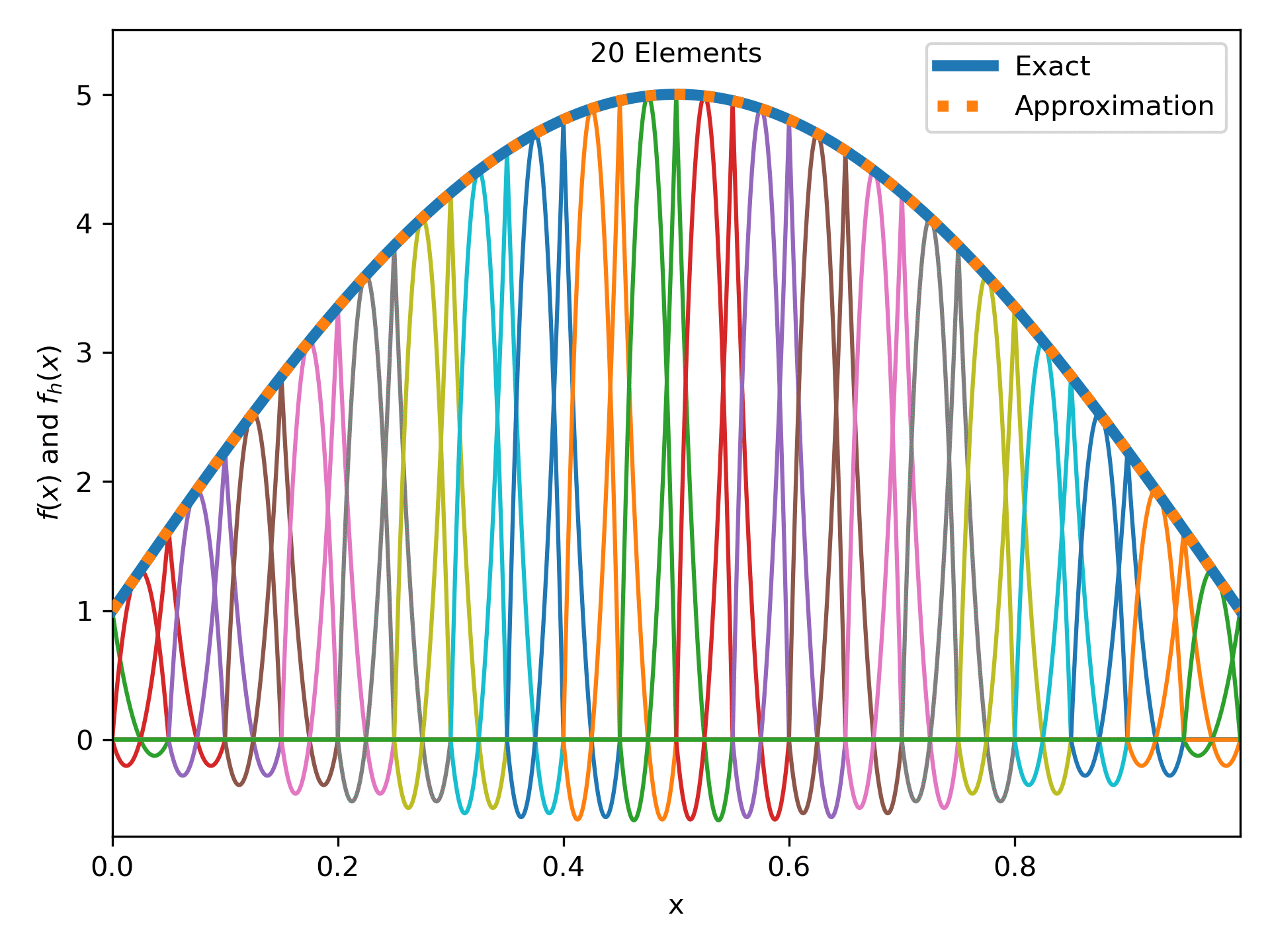
Fig. 15 : The function \(4\sin(\pi x) + 1\) approximated more and more quadratic elements.

Fig. 16 : The approximation of \(f(x)\) with quadratic elements.

It is important to notice from Fig. 16 that the resulting curve is not smooth. for example at \(x=0.5\) one can see that the red approximation (6 elements) is non-smooth.

2.2.3 Comparison

For the comparison of these different approximations I’ve plotted the errors on a log scale. Please do note that the quadratic elements have \((N+1)N\) unknowns where the linear elements have \(N+1\) weights to be determined. Nevertheless there is no interdependency between these weights, which as mentioned before means that these can be determined independently.

Fig. 17 : The error \(E_1\) for our element based approximations with 1 to 20 elements.

Fig. 18 : The error \(E_2\) for our element based approximations with 1 to 20 elements.

The script used for these computations can be found at 4 LocalApproximation.py.